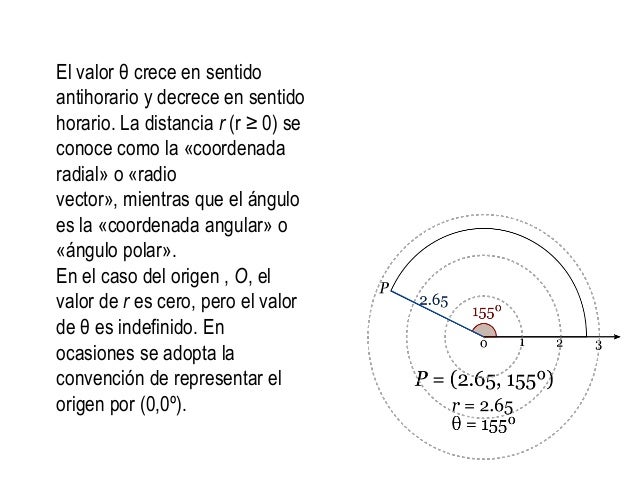
Ecuaciones en sistemas polares

Ecuaciones en sistemas polares

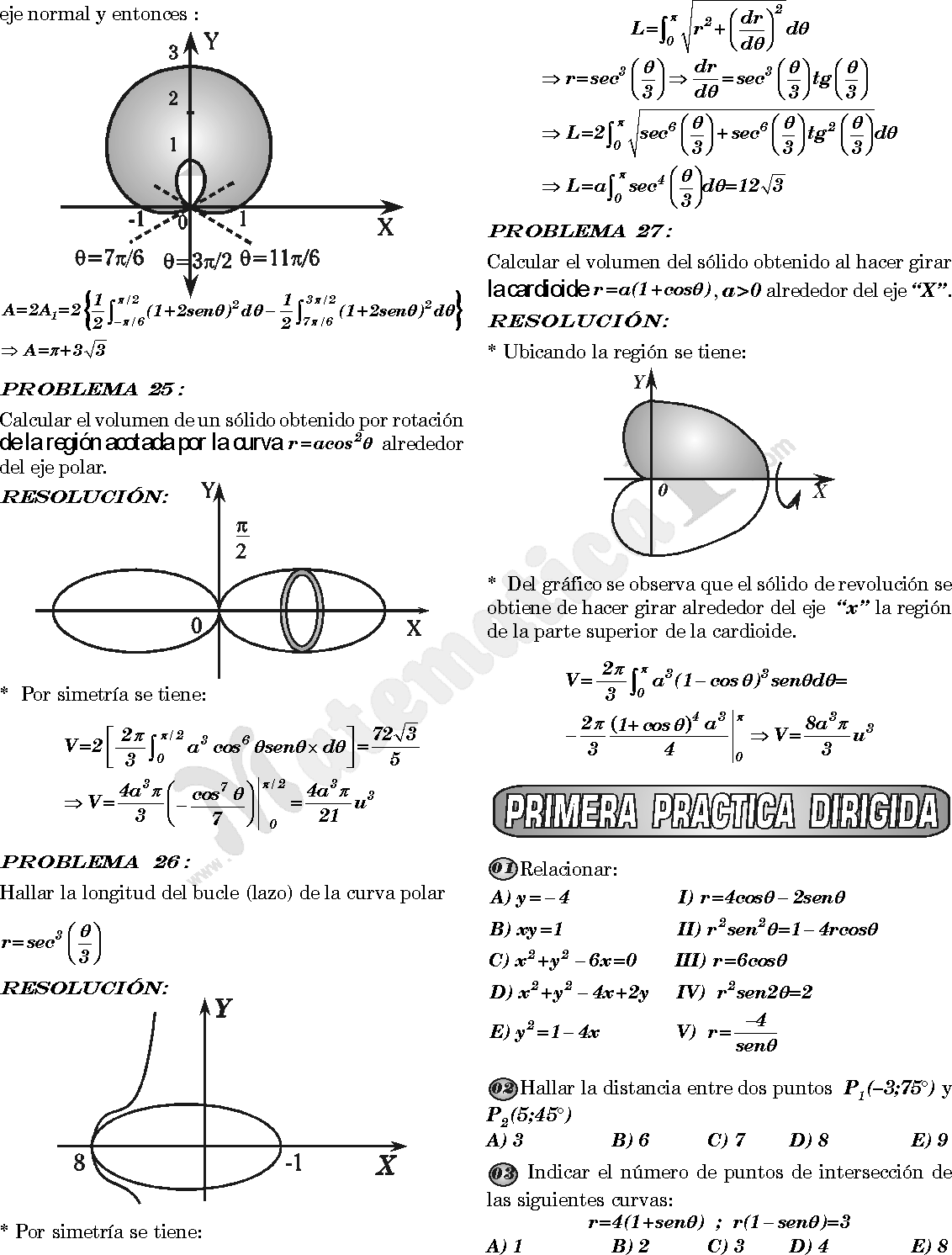
Objetivo: Graficar caracoles, rosas, lemis cartas, y espirales en sistema polar.
Para graficar una ecuación se debe tener una variable independiente en el sistema polar, la variable dependiente es generalmente el angulo, los principales lugares geométricos (casos especiales) son:
Caracoles, rosas, lemis cartas y espirales.
Ejemplo:

Sistema polar

Sistema polar

Un sistema rectangular se compone con ejes perpendiculares que cuentan con proyecciones para ubicar un punto en el plano, sistema solar cuenta con círculos concentricos que representan la magnitud radios homogéneos que representa el angulo de inclinación para calcular un punto en ordenadas polares que utilizan las siguientes ecuaciones.

Hiperbola

Hipérbola

Identificar los elementos de la hipérbola fuera del origen:
Cuando una hipérbola no se encuentra en el origen sus elementos se representan en función del centro como muestran los siguientes esquemas:

HIPERBOLA

HIPERBOLA:

Identificar los elementos de la hiperbola
  

ELIPSE

Elipse

Objetivo: Identificar los elementos de la elipse.
Una elipse se define por una cónica formada cuando se realiza un corte en diagonal a un cono, en forma análoga a la parábola es una cónica formada por dos parábolas que cuentan con el mismo eje simétrico y su concavidad es opuesta.
Sus elementos importantes son:
a) Vértice
b) foco
c) lado recto
d) eje mayor (distancia entre vértices)
e) eje menor (ancho de la parábola)
f) excentricidad
g) directriz


Para calcular los elementos de una parábola cuando el centro se encuentra en el origen.
Se deben identificar los valores de la distancia focal, la distancia del foco al centro y la distancia del centro al eje menor (a,b,c) las ecuaciones matemáticas utilizadas en esta cónica se representan el el siguiente esquema.

ELIPSE

Elipse

Objetivo: identificar la ecuación de la elipse
Una elipse es el lugar geométrico que se forma a partir de un corte diagonal un cono.
su ecuación se define como una ecuación cuadrática donde la variable dependiente e independiente son de segundo grado de diferente coeficiente y de signo positivo.
las siguientes ecuaciones representan en forma gráfica, lugares geométricos, cíclicos. ¿Cual de ellas son elipses?


Ejemplo
x²+y²=4 se despeja y


y=√ 4-x² después de despejar y se resuelve de la siguiente manera:


x y
-3 0
-2 0
-1 ± 1.7320
0 ± 2
1 ± 1.7320
2 0
3 0 se sustituye el numero de la "x" en la ecuación ya despejada


Realizaremos la gráfica y sabremos si es una elipse.

                                                                                               

PARABOLA

Parábola

Identificar la ecuación de una parábola con centro en el origen.

X2-8y=0

Ejercicios:

Para calcular los elementos de una parábola con vértice en el origen debemos identificar el valor de la distancia focal "P" los elementos importantes de una parábola son:

Las ecuaciones para calcular los elementos de una parábola con el vértice en el origen son:

Ejemplo:

Ejercicio: Parábola con vértice en el punto (1,3)y todo recto horizontal de 16 u con una abertura negativa indique su ecuación general y grafiquela.