Ecuaciones en sistemas polares

Ecuaciones en sistemas polares

Objetivo: Graficar caracoles, rosas, lemis cartas, y espirales en sistema polar.
Para graficar una ecuación se debe tener una variable independiente en el sistema polar, la variable dependiente es generalmente el angulo, los principales lugares geométricos (casos especiales) son:
Caracoles, rosas, lemis cartas y espirales.
Ejemplo:

Sistema polar

Sistema polar

Un sistema rectangular se compone con ejes perpendiculares que cuentan con proyecciones para ubicar un punto en el plano, sistema solar cuenta con círculos concentricos que representan la magnitud radios homogéneos que representa el angulo de inclinación para calcular un punto en ordenadas polares que utilizan las siguientes ecuaciones.

Hiperbola

Hipérbola

Identificar los elementos de la hipérbola fuera del origen:
Cuando una hipérbola no se encuentra en el origen sus elementos se representan en función del centro como muestran los siguientes esquemas:

HIPERBOLA

HIPERBOLA:

Identificar los elementos de la hiperbola
  

ELIPSE

Elipse

Objetivo: Identificar los elementos de la elipse.
Una elipse se define por una cónica formada cuando se realiza un corte en diagonal a un cono, en forma análoga a la parábola es una cónica formada por dos parábolas que cuentan con el mismo eje simétrico y su concavidad es opuesta.
Sus elementos importantes son:
a) Vértice
b) foco
c) lado recto
d) eje mayor (distancia entre vértices)
e) eje menor (ancho de la parábola)
f) excentricidad
g) directriz


Para calcular los elementos de una parábola cuando el centro se encuentra en el origen.
Se deben identificar los valores de la distancia focal, la distancia del foco al centro y la distancia del centro al eje menor (a,b,c) las ecuaciones matemáticas utilizadas en esta cónica se representan el el siguiente esquema.

ELIPSE

Elipse

Objetivo: identificar la ecuación de la elipse
Una elipse es el lugar geométrico que se forma a partir de un corte diagonal un cono.
su ecuación se define como una ecuación cuadrática donde la variable dependiente e independiente son de segundo grado de diferente coeficiente y de signo positivo.
las siguientes ecuaciones representan en forma gráfica, lugares geométricos, cíclicos. ¿Cual de ellas son elipses?


Ejemplo
x²+y²=4 se despeja y


y=√ 4-x² después de despejar y se resuelve de la siguiente manera:


x y
-3 0
-2 0
-1 ± 1.7320
0 ± 2
1 ± 1.7320
2 0
3 0 se sustituye el numero de la "x" en la ecuación ya despejada


Realizaremos la gráfica y sabremos si es una elipse.

                                                                                               

PARABOLA

Parábola

Identificar la ecuación de una parábola con centro en el origen.

X2-8y=0

Ejercicios:

Para calcular los elementos de una parábola con vértice en el origen debemos identificar el valor de la distancia focal "P" los elementos importantes de una parábola son:

Las ecuaciones para calcular los elementos de una parábola con el vértice en el origen son:

Ejemplo:

Ejercicio: Parábola con vértice en el punto (1,3)y todo recto horizontal de 16 u con una abertura negativa indique su ecuación general y grafiquela.

PROBLEMAS DE PALICACION

PROBLEMAS DE APLICACIÓN.

Para resolver un problema de aplicaciones se debe diseñar un esquema que muestre gráficamente los valores del problema y posteriormente indicar el modelo matemático del problema.

Ejemplo:
Un edificio de 40mts. de altura, donde su punto mas alto con otro edificio es de 32mts. de altura que se encuentra separado a una distancia de 50mts. Indique la ecuación pendiente al origen que describe la unión de dos edificios, Indique la altura recta a 10mts. del edificio mas alto.

Ejemplo:Un cañón dispara una bala con un angulo de inclinación de 30°. Indique la ecuación de la trayectoria de la bala , indique la altura de la bala si horizontalmente recorre 700 mts .Indique la distancia horizontal recorrida cuando alcanza una altura de 100 mts.

Una casa tiene una altura de 2 mts y se coloca una escalera de su lado derecho para descender a su nivel del suelo , si la longitud de la base de la casa a la base de la escalera es de 3 mts ; indique la ecuación pendiente ordenada al origen de la escalera.

PROBLEMAS DE CIRCUNFERENCIA

Problemas:

Una rueda de la fortuna tiene un diámetro de 18 mts. y su centro se encuentra a 10 mts sobre el nivel del suelo. Indique la altura de las canastillas a tres mts a la izquierda del centro , indique a que distancia horizontal de la base se puede encontrar una canastilla con una altura de 12 mts.

Ejemplo:Un barco se encuentra 30 km al norte y 70 km al este y cuenta con un radar que tiene un alcance máximo de 50 km ; indique la ecuación general que representa el radar .

Si un barco se encuentra al limite del radar indique su posición en el plano cartesiano.

Ejercicio:

Una autopista tiene forma circular alrededor de una ciudad que se encuentra a 70 km al oeste y 10 km al sur, el diámetro de la autopista es de 50 km, si un auto se descompone a 20 km al norte y al oeste de la ciudad indique:

a)La ecuación general de la autopista 

b)La ubicación del automóvil descompuesto

ELEMENTOS DE LA CIRCUNFRENCIA

Circunferencia:

Identificar los elementos de una circunferencia con centro fuera del origen.

Ejemplo:Indique la ecuación de la circunferencia X2+Y2 =10x+8y+5=0 grafiquela e indique el valor de las ordenadas cuando las abscisas valen 3u.

Ejercicio e indique el valor de las abscisas , las ordenadas valen -2 unidades de la circunferencia X2+Y2+2x-8y-8=0.

ECUACION DE LA CIRCUNFERENCIA

Circunferencia:

La ecuación de la circunferencia con centro fuera del origen se determina por la ecuación:

 

Ejemplo:Indique la ecuación cónica y general de la circunferencia con centro en el punto 4,2 y r = 3.Grafiquelo.

Ejercicio: Grafique y calcule la circunferencia con centro en el punto (-1,-2) y pasa por el punto (2,29 indique la ecuación general y canónica.

CIRCUNFERENCIA

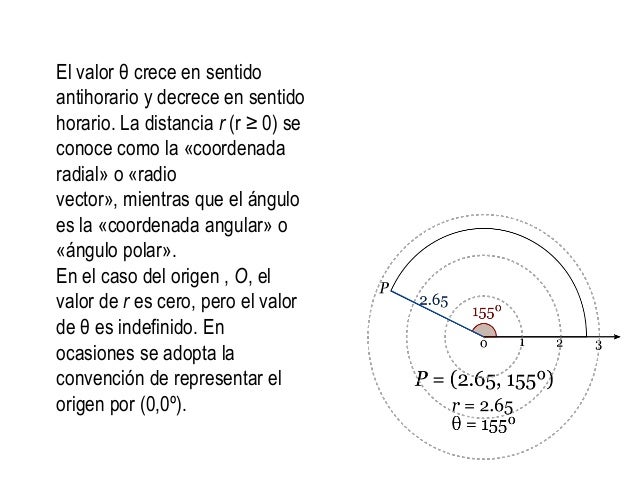
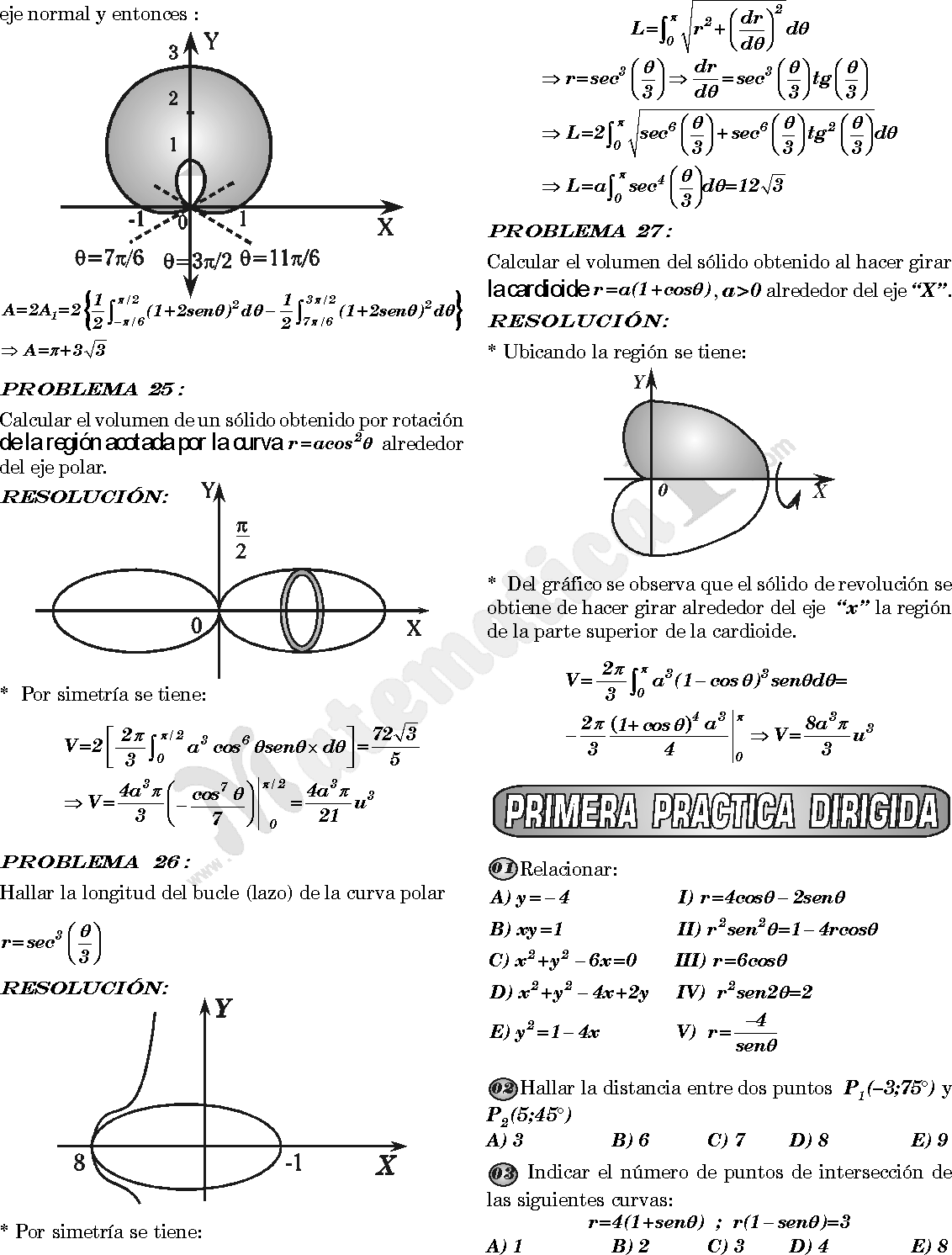
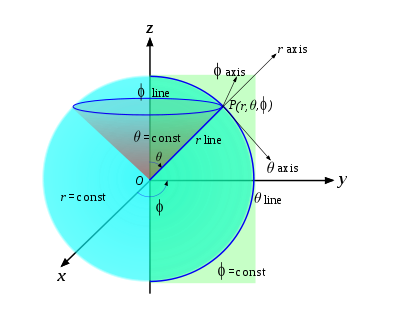
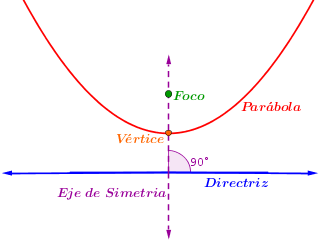
Circunferencia:

Identificar la ecuación de la circunferencia con centro en el origen.

Las cónicas se definen como aquellos lugares geométricos que se forman aparir de cortes realizados a un cono, si el cono se corta en forma horizontal se obtiene una circunferencia, si el corte se realiza en forma diagonal se obtiene una elipse , si el corte se realiza vertical se obtiene una parábola , si el corte se realiza con dos conos concentricos se obtiene una hipérbola.

Una circunferencia de define como el lugar geométrico formado por puntos equilistantes a un punto llamado centro de la distancia entre el centro y cualquier punto, se denomina radio.

Cundo una circunferencia tiene su centro en ele origen se representa matemáticamente con la siguiente ecuación.

Ejemplo: Grafique la circunferencia X2+Y2 = 6.25

Ejemplo:Encuentre la ecuación canónica y general de la circunferencia que pasa por el punto 2,-6 indique la altura de la circunferencia ,3 cm a la derecha de su centro.

Ejercicio:Una circunferencia pasa por el punto 2,4 indique su ecuación general y canónica , el valor de las abscisas (x) cuando se tiene una altura de 1.5 cm.

FORMA REDUCIDA

Forma reducida:

El valor de A y B indican el punto donde la recta corta a los ejes coordenados , graficamente significa:

Ejemplo :Indique en todas sus formas a la recta que pasa por sus puntos 3,2 y 6,-1.

Ejercicio : Represente en todas sus formas a la siguiente recta y grafiquela.

RECTA

Recta:

Punto pendiente para representar una recta conociendo un punto por donde pasa y la pendiente o angulo de inclinación se utiliza la ecuación.
(y-y1) = m (x-x1)
Aparir  de esta ecuación se pueden encontrar las ecuaciones restantes como indican los siguientes ejemplos.

1)Grafique la recta que pasa en el punto 3,8 y cuenta con angulo de inclinación de 45°.

Ejemplo: Grafique la recta (Y-3) =1/3 (X +5) represente en la forma pendiente ordenada al origen y general.

Ejemplifique y represente en la forma punto pendiente a la recta.

AREA DE UN POLIGONO

Área de un polígono:

Para calcular el aérea de un polígono conociendo sus vértices se realiza una determinante con cada una de ellos matemáticamente se puede expresar con la siguiente ecuación:

A=  X1 Y2

       X2 Y2

       X3 Y3

       Xn Yn

       Xn Yn

Calcule el área del siguiente triangulo formado por los puntos a(-1,-2) b(-1,2) c(1,1).

Ejemplo:Indique el área del polígono formado por los siguientes puntos:

Calcule el área y perímetro del siguiente cuadrilátero:

Ejercicio: Calcule el área y perímetro de los siguientes polígonos:

Ejercicio 2: